Ziffer

Die Zahl 380 in den verschiedenen Zahlensystemen

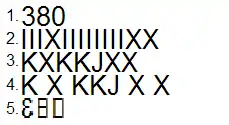
1. Neuzeitliche Schreibweise
2. Ur-Archimedisches Rechensystem,
3. Ur-Archimedisches Rechensystem Ordnung
4. Ur-Archimedisches Rechensystem Ordnung 2b
5. Gräfisches Zahlensystem

Archimedes hat das erstemal das Wort "Ziffer" im Jahre 5 vor seiner Erschaffung der Urnull. Ihr alten Ziffern waren da noch in Mengenschreibweise. Er hat die Zahl in immer eine Ziffer eingeteilt, und diese dann notiert: z.B. 345 wäre nach dem Ur-Archimedeschen Rechensystem IIIIIXIIIIXIII. Er hat also jede Ziffer (von rechts nach links) notiert, nach dessen Wert, und untereinander mit einem "X" abgetrennt. So kam es dann bei den Römern dazu, dass das Zeichen "X" gleichbedeutend mit 10 ist.

Im Jahre drei vor hat er dann das Zahlensystem revolotioniert:

• 1 = I
• 2 = J
• 3 = K
• 4 = KI (JJ ist unzulässig)
• 5 = KJ
• 6 = KK
• 7 = KKI (KJJ is unzulässig)
• 8 = KKJ
• 9 = KKK

Dabei gab es folgende Regeln:

• Kürzeste Schreibweise (wenn es 2 Stellig geht, dann ist 3 stellig unzulässig).
• Die erste Hälfte der Zeichen muss so groß wie möglich sein (siehe 4 und 7), wobei der mittlere Wert bei einer ungeraden Länge halbiert wird.
• Es gibt keine weiteren Ziffern (Der Rest, wird ähnlich dem Ur-Archimedeschen Rechensystem notiert).

Dieses System bekam den Namen: "Ur-Archimedisches Rechensystem Ordnung 2" Die 345 von oben wird damit folgendermaßen notiert: KXKIXKJ Ein paar Monate später gab es die Ergänzung, dass es erlaubt ist, dass "X" hervorzuheben. (Das Beispiel: K X KI X KJ)

Im Jahre 0 dann, nach der Entwicklung der Urnull, kam die "0" dazu. Er schrieb sie eher Kastenförmig. Aber alle konnten die Null erkennen, wenn sie wenigstens so ähnlich aussah. Die Notation bieb die gleiche. Allerdings wurde dieses System manchmal "Ur-Archimedisches Rechensystem Ordnung 2b" genannt.

Erst mit Graf Zahl konnte sich, nachdem er an den kaputten Zahlen gescheitert ist (Was wahrscheinlich an der geringen Sportlichen Begabung mit den Ziffern lag) das "arabische" Zahlensystem durchsetzten, so wie es heute üblich ist. Die Zahlen waren allerdings teilweise verändert:

• Die 3 sah wie ein Epsilon aus (ε).
• Die 0 war immer noch ein Rechteck.
• Die 8 Sah wie die 0 aus, nur mit einem Querstrich.

Da dieses System ähnlich dem arabischen ist, wurde es "arabisches System" genannt. Aber es war auch Ziffernraum, KRZ (kantig und rund Ziffern) gebräuchlich. Zu Ehren von Graf Zahl wurde es dann bald auch "Gräfisches Ziffernsystem" genannt, oder "Neu-Archimedisches Rechensystem".

Das heutige System ("Neu-Gräfisches Ziffensystem" oder "Jetzt-Archimedesches Rechensystem") ist das System, so wie wir es kennen. Allerdings lehnt Graf Zahl dieses System ab, oder die Bezeichnung, es sei ein Archimedisches System. Die meisten Mathematiker vermuten, es läge daran, dass Graf Zahl das System für sich beansprucht. Graf Zahl wieder rum lehnt dieses Vorurteil ab.

• Wenn man die 0 nicht betrachtet, dann ist die Neuzeitliche Verteilung rund/kantig 1 zu 3, was in Prozent ausgedrückt zwei Reinst unendliche Überkaputte Zahlen sind (33,3333 und 66,6666)
• Die 0 ist die schönste Zahl: Sie ist die rundeste aller, und mit einem leichten Bogen zu zeichnen
• Alle Neuzeitlichen Ziffern können in einem Zug gezeichnet werden

• Ziffernraum
• Kaputte Zahlen
• Archimedes
• Graf Zahl