Diverses:Wasserstoffbrückenbau am absoluten Nullpudding
Unter strengsten Sicherheitsvorkehrungen werden Schutzbrille, Kittel, Gummihandschuhe und Schutzscheibe gleichmäßig und behutsam auf eine Wasseroberfläche gegeben. Anschließend wenden wir uns dem Pudding zu.

Theorie
Stellen wir uns vor, ein Physiker läuft einmal um den Pudding, um ihn anschließend zu essen: Wird er insgesamt mehr Energie aufnehmen oder verbrauchen? Rein mathematisch betrachtet lässt sich diese Frage recht elegant lösen – die Antwort lautet: „Kommt darauf an.“ (Für den ausführlichen Beweis siehe Grenzwertbetrachtung am Pudding.)
Dieses äußerst interessante Ergebnis soll noch ein wenig präzisiert und sodann im praktischen Experiment vorgeführt werden.
Bei welcher Größe gilt Gleichheit?
Art und Weise der Problemstellung legen folgenden Ansatz nahe:
- [math]E_U = B_P \Leftrightarrow U \cdot \eta = V \cdot \rho \cdot \omega[/math] ,
wobei [math]E_U[/math] die eingesetzte Energie ist und [math]B_P[/math] der Brennwert des Puddings, [math]U[/math] der Umfang und [math]V[/math] das Volumen des Puddings, [math]\eta[/math] die Energie pro Strecke, die der Physiker beim Laufen aufwendet (in populärwissenschaftlichen Publikationen gern euphemistisch als Arbeit bezeichnet), [math]\rho[/math] die Dichte des Puddings und schließlich [math]\omega[/math] der Nährwert pro Masse (des Puddings, nicht des Physikers).
Diesen Pudding, dessen Energiegehalt identisch mit der Energie ist, die für den einmaligen Umlauf aufgewendet werden muss, bezeichnen wir im Folgenden als Umschlagpudding, denn anhand der Formel ist auf den ersten Blick klar, dass jeder kleinere Pudding eine negative Energiebilanz aufweist und jeder größere eine positive; er markiert mithin den Punkt, an dem die Energiebilanz umschlägt.
| Handelsübliche Werte | |
|---|---|
| Geschwindigkeit | 10 km/h |
| Masse | 80 kg |
| Kraftaufwand | 300 N |
| Dichte | 0,8 g/cm3 |
| Brennwert | 9,2 kJ/g |
Wir gehen selbstverständlich davon aus, dass der Pudding kugelförmig ist. Damit gilt für Umfang und Volumen:
- [math] U = 2 \pi r, \; V = \frac 4 3 \pi r^3[/math]
Durch simple Termumformungen und Einsetzen handelsüblicher Werte (vgl. Tabelle rechts) erhalten wir:
- [math]2 \pi r \cdot 300 \, \mathrm{\frac{J}{m}} = \frac 4 3 \pi r^3 \cdot \mathrm{0{,}8 \, \frac{g}{cm^3} \cdot 9{,}2 \, \frac{kJ}{g}}[/math]
- [math]\Rightarrow 450 \, \mathrm{\frac{J}{m}} = r^2 \cdot \mathrm{7{,}36 \, \frac{kJ}{cm^3}}[/math]
- [math]\Rightarrow r^2 = \mathrm{\frac{450 \, \frac{J}{m}}{7{,}36 \, \frac{kJ}{cm^3}} = \frac{450 \, cm^3}{7360 \, m} \approx 0{,}0611 \, mm^2}[/math]
- [math]\Rightarrow r \approx \mathrm{0{,}247 \, mm}[/math]
Daraus ergeben sich etwa 50 µg Masse und ein Brennwert von 469 mJ* für den Pudding. Der Physiker läuft insgesamt eine Strecke von rund 1,6 mm, die er in 580 µs zurücklegt.
Auf den Laien mögen diese Zahlen zunächst etwas enttäuschend wirken. In Wahrheit sind sie aber überraschend günstig. Es hätte ebenso gut ein Radius im subatomaren Bereich werden können oder ein Gewicht, das am besten in Sonnenmassen angegeben werden kann. So einen Pudding will aber keiner essen.
Dagegen ist ein knapper halber Millimeter Durchmesser ein Wert, mit dem man hervorragend arbeiten kann. Der Pudding ist mit bloßem Auge gerade noch zu erkennen und kann unter Umständen sogar mit Hausmitteln hergestellt werden. Und eine Strecke von weniger als zwei Millimetern ist leicht fußläufig zurückzulegen, wie wir im praktischen Experiment bald unter Beweis stellen werden.
* 0,0448 ppm der empfohlenen Tageszufuhr
Definition: Absoluter Nullpudding
Der absolute Nullpudding [math]P_0[/math] (in älterer Literatur gelegentlich Minimalpudding, Symbol: [math]P_M[/math] ) ist definiert als der kleinste überhaupt mögliche Pudding. Mathematisch formalisiert heißt das:
- P ist genau dann ein absoluter Nullpudding, wenn für jedes beliebig kleine Stück e von P gilt: [math]P \setminus e[/math] ist kein Pudding mehr.
Oder, äquivalent dazu, aber etwas positiver formuliert:
- P ist genau dann ein absoluter Nullpudding, wenn für jedes beliebig kleine Stück e von P gilt: [math]e = P[/math] .
Konstruktion des absoluten Nullpuddings
Rein pragmatisch war es bis zu Beginn des letzten Jahrhunderts nicht möglich, Puddinge mit weniger als einem Millimeter Durchmesser zuzubereiten, weil einfach die handwerklichen Mittel dazu fehlten. Pudding ist unter Standardbedingungen ein recht viskoses Material mit hoher Adhäsion, das in hinreichend kleine Öffnungen kaum hineinzuführen ist und wenn doch, dann ist es anschließend umso schwerer wieder zu entnehmen. Das ist nebenbei bemerkt auch der Grund dafür, dass Pudding traditionell nicht einfach durch die Poren der Haut aufgenommen, sondern oral zugeführt, also gegessen wird, was zunächst sehr unnötig und umständlich erscheint. Bevor wir mit der Planung des praktischen Experiments beginnen, werfen wir noch einen kurzen Blick auf die zwei unterschiedlichen Wege zur Konstruktion des absoluten Nullpuddings.
Top-down

Mit Hilfe der fortschreitenden Mikrotechnologie erfuhr die Miniaturisierung des Puddings in den letzten Jahrzehnten einen enormen Schub, so dass es inzwischen gelungen ist, so genannte Mikropuddinge mit wenigen Mikrometern Durchmesser im industriellen Maßstab herzustellen und mit befriedigenden Absatzzahlen am Markt zu platzieren. Üblicherweise werden mehrere Millionen Mikropuddinge in Tütchen abgefüllt und gelangen unter der Trivialbezeichnung „Puddingpulver“ in die Haushalte. Aufgrund der wesentlich größeren Reaktionsfläche wird Puddingpulver vom Körper sehr viel schneller aufgenommen als massiver Pudding und wirkt daher als starkes Stimulans mit hohem Abhängigkeitspotential. Häufig wird das Produkt jedoch völlig missverstanden und einfach wieder zu einem einzigen großen Pudding zusammengekocht.
Mit dem Aufkommen der Nanotechnologie ergaben sich nicht nur neue Möglichkeiten für mikroskopisch kleine Puddinge, sondern es stellte sich auch die Frage, ob es für deren Größe überhaupt eine prinzipielle Untergrenze gibt oder nur die jeweils praktische, die sukzessive überwunden werden könnte. Dass ein absoluter Nullpudding überhaupt existiert, ist aus der mathematischen Definition nicht herleitbar und auch aus der Anschauung heraus nicht unmittelbar einsichtig.
Bottom-up
Anstatt den Nullpudding durch Teilung eines größeren Puddings zu erreichen, können mit heutigen Mitteln auch umgekehrt einzelne Teilchen zu einem Nanopudding zusammengefügt werden. Dazu müssen lediglich Bausteine gefunden werden, die ganz sicher kleiner sind als der kleinste Pudding. Bleibt noch die Frage zu klären, ob es solche überhaupt gibt. Warum sollte es keine beliebig kleinen Puddinge geben?
Ohne unnötig weit auszuholen, lässt sich diese Frage am besten über den historischen Umweg durch die Weltanschauung der alten Griechen vor über zweitausend Jahren beantworten. Schon damals glaubten die Philosophen, das Essen sei aus unteilbaren, kleinsten Bausteinen aufgebaut, die sie Portionen nannten. Das glauben wir auch heute noch. In der Zwischenzeit haben sich die vermeintlich kleinsten Bausteine der Materie zwar doch noch als teilbar erwiesen (vor allem in Japan), das zugrunde liegende Argument bleibt davon jedoch unberührt: Es gibt kleinste Teilchen, die sich nicht mehr weiter teilen lassen, und der Pudding kann schlechterdings nicht noch kleiner sein.
Tatsächlich ist der absolute Nullpudding wahrscheinlich deutlich größer als ein handelsübliches Elementarteilchen. Ein Proton zum Beispiel ist kein Pudding: Erstens, weil es geladen ist, und der Pudding per Definition elektrisch neutral ist, und zweitens besteht es nur aus drei Quarks und zählt daher zu den Quarkspeisen.
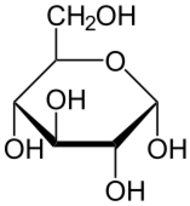
Inzwischen herrscht weitgehende Einigkeit darüber, dass ein Pudding mindestens süß und elastisch sein muss, um als Pudding gelten zu können. Damit ist der frühere Ansatz, den absoluten Nullpudding mit dem Kohlenstoffatom zu identifizieren, hinfällig. Stattdessen deutet nach heutigem Stand der Wissenschaft alles darauf hin, dass das α-D-Glucopyranose-Molekül (Abbildung rechts) die Definition am besten erfüllt.
Versuchsaufbau
Bevor wir nun unseren Physiker um einen geeigneten Pudding laufen lassen und anschließend seine Energiebilanz untersuchen, müssen wir noch ein paar letzte Vorüberlegungen zum Thema Mechanik leisten.
Eine Kreisbewegung, wie sie der Physiker im praktischen Experiment vollführen soll, enthält neben der bisher untersuchten Translationsbewegung noch eine zweite Komponente, nämlich eine Drehung um die eigene Achse, die wir zunächst vernachlässigt haben. Dies ist genau solange legitim, wie der gelaufene Kreis sehr groß im Vergleich zum Umfang des Physikers ist. Je kleiner der Kreis wird, desto ungünstiger entwickelt sich das Verhältnis von Rotation und Translation. Da der oben entwickelte Umschlagpudding einen Umfang von weniger als zwei Millimetern hat, wird die Bewegung des Physikers eher einer Piroutte gleichen, die er in nur 580 Mikrosekunden über die Bühne bringt. Das entspricht einer Winkelgeschwindigkeit von über 10800 rad/s und bewirkt in Verbindung mit einem geschätzten Umfang von mindestens einem Meter an der Gürtellinie eine überraschend hohe Zentrifugalbeschleunigung in den Außenbereichen des Physikers, die wir keinesfalls ignorieren dürfen.
Die Beschleunigung am Äquator des Physikers berechnet sich wie folgt:
- [math]U \approx \mathrm{1\,m \Rightarrow r \approx \frac{1}{2 \pi} \approx 0{,}159\,m}[/math]
- [math]v \approx \mathrm{\frac{1\, m}{0{,}00058\, s} \approx 1724 \frac{m}{s}}[/math]
- [math]\Rightarrow a = \frac{v^2}{r} \approx \mathrm{\frac{(1724 \, \frac{m}{s})^2}{0{,}159\,m} \approx 1{,}9 \cdot 10^{7} \, \frac{m}{s^2}}[/math]
Das ist beinahe die zweimillionenfache Erdbeschleunigung und würde offensichtlich dazu führen, dass er augenblicklich in Stücke gerissen wird. Das ist für den Versuchsaufbau natürlich denkbar ungünstig, denn wenn der Physiker allein durch die Fliehkraft einen Großteil seiner Masse verliert, verfälscht das die anschließenden Messergebnisse enorm und nimmt ihnen jeden wissenschaftlichen Wert. Damit ist das Experiment hinfällig.